2011年台湾亚东技术学院的潘文超受果蝇觅食行为的启发，提出了一种的全局优化算法—果蝇优化算法（Fruit Fly Optimization Algorithm，FOA）。该算法的优点在于计算过程简单、易于编码实现和易于理解等。

启发

果蝇本身在感觉和感知方面优于其他物种，尤其是在嗅觉和视觉方面，如下图所示。

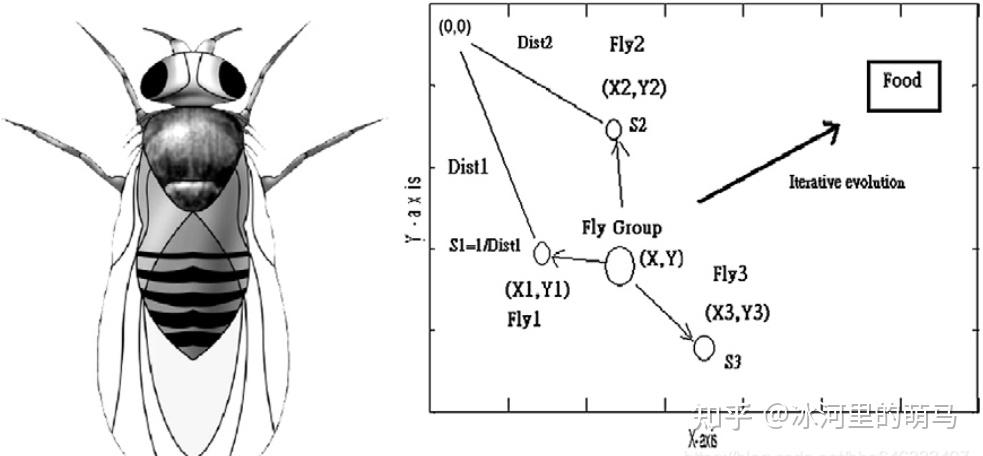
果蝇的嗅觉器官能发现空气中漂浮的各种气味;它甚至能闻到40公里外的食物。然后，当它接近食物位置，也可以用它灵敏的视觉找到食物和同伴聚集的位置，并朝那个方向飞行。

初始化

首先随机初始化果蝇种群位置 和 。

食物搜索

通过嗅觉给出果蝇寻找食物的随机方向和距离：

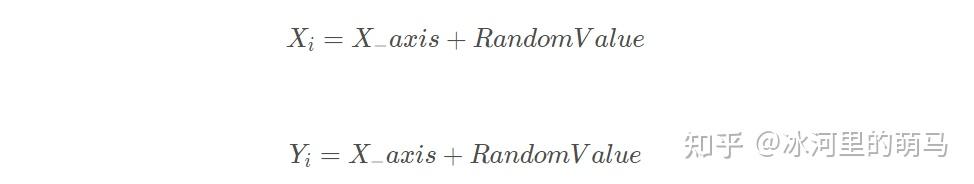
计算味道浓度判定值

由于无法得知食物位置，因此先估计与原点的距离 ，再计算味道浓度判定值 ，此值为距离倒数：

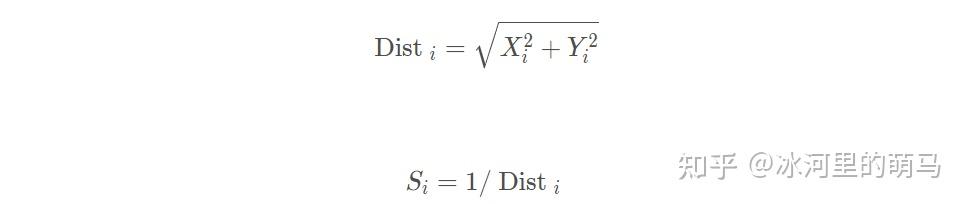
适应度评估

将味道浓度判定值 ，代入味道浓度判定函数(或称为适应度函数fitness function)，用来求出果蝇个体位置的味道浓度 。

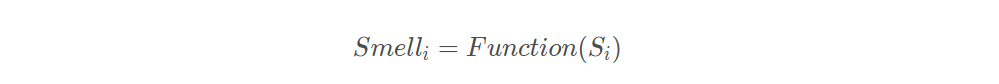
确定最优个体

找出该果蝇群体中味道浓度最低的果蝇(最优个体)；

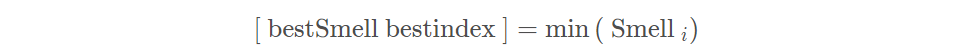
记录并保留最佳味道浓度值bestSmell与其x、y坐标，此时果蝇群体利用视觉向该位置飞去：

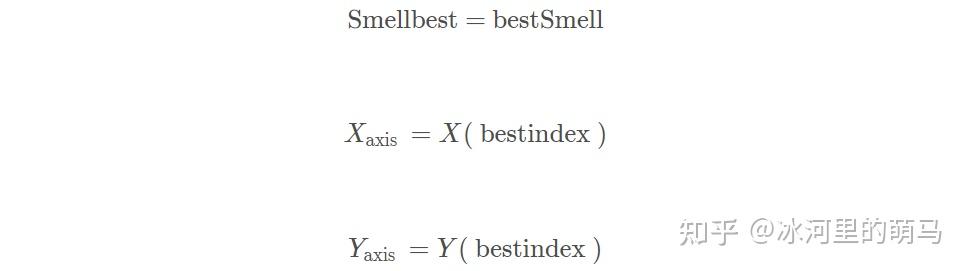
重复执行食物搜索、计算味道浓度判定值、应度评估、定最优个体，并判断最佳味道浓度是否优于前一迭代最佳味道浓度。若当前迭代次数小于最大迭代数Maxgen，则执行飞行。结果如下。

原理

蝙蝠算法（Bat Algorithm，BA）是一种基于群体智能的算法，是受微型蝙蝠的回声定位的启发，由Xin-She Yang (Yang, 2010a)于2010年提出的。大多数微型蝙蝠将声音辐射到周围环境，并聆听这些声音来自不同物体的的回声，从而可以识别猎物，躲避障碍物，并追踪黑暗的巢穴。声音脉冲因蝙蝠的种类而异，基本上，频率调谐是一种突变，因为它在解中引起波动，主要是在较好的解附近，尽管较大的突变导致全局搜索。特定的选择是通过对相对恒定的选择施加压力来实现的，这是由于在目前已经建立的种群中使用了最优解。与遗传算法相比，没有明显的交叉;然而，响度和脉冲发射的偏差会导致变异的不同。另外，还有一种自动缩放的功能，即随着搜索在响度和脉冲发射率的变化上接近全局最优，利用就会变得集中起来，这导致从探索阶段自动切换到利用阶段。

蝙蝠的自然行为概述

蝙蝠是唯一有翅膀的哺乳动物，它们具有非凡的回声定位能力。它们是世界上种类第二多的哺乳动物，有超过1200种。一般分为蝙蝠可以分为两类：回声定位微型蝙蝠和以水果为食的巨型蝙蝠。蝙蝠算法是由Yang Xin-She (2010a)[1]基于第一类蝙蝠的行为而开发的。大多数蝙蝠以倒挂的栖息姿势休息。所有的微型蝙蝠和一些巨型蝙蝠都会发出超声波来产生回声。微型蝙蝠的大脑和听觉神经系统可以通过比较出站脉冲和反复出现的回声，对环境产生深入的图像。微型蝙蝠发出这些超声波(通过喉部产生)通常通过嘴巴，偶尔通过鼻子，它们会在回声返回前就结束发出超声波。回声定位可以是低负荷循环，也开始是高负荷循环，第一种情况时，蝙蝠可以根据时间区分它们的叫声和多次出现的回声；第二种情况时，蝙蝠发出不间断的叫声，并在频率上将脉冲和回声分离。回声定位也被称为生物声纳，主要用于动物的导航和觅食。在这些回声的帮助下，蝙蝠测量物体的大小和距离，有些种类的蝙蝠甚至能够测量物体移动的速度。

蝠算法的数学表达

蝙蝠在寻找目标、对象或猎物时，在位置xi以速度vi随机飞行，其具有静态的频率fmin变化的波长λ，响度A0。频率变化范围为fmin到fmax，声音的响度可以根据需要在A0和Amin之间变化。Xin-She Yang (2010a)建立了一系列规则来更新蝙蝠寻找猎物时的速度、位置和响度。蝙蝠算法的数学公式如下：

其中β为[0,1]内均匀分布的随机数，x*表示当前种群中的全局最优解，r为脉冲发射率，α和γ为常数且0<α<1，γ>0。

选择全局最优解后，当前种群中每一个局部解（xold）使用式（6）更新其位置：

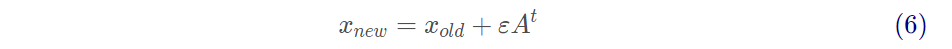
其中ε为[-1,1]之间的任意数。

BA结合了粒子群优化、遗传算法和和声搜索的最佳特性，因此，与这些算法相比，它提供了良好的结果。参数α和γ的调整会影响收敛速度。BA的实现有点复杂，但它已经证明了它的性能，并称为一种良好的受自然启发的元启发式。

算法流程

步骤1: 参数初始化：蝙蝠种群规模m，迭代次数N，目标函数 ，蝙蝠位置 和速度 ，声波频率 ，声波响度 和频度 。

步骤2: 找出当前种群中最优蝙蝠位置 ，并根据公式（2）~（4）更新速度和位置。

步骤3: 生成随机数 ， 是[0，1]上的随机数。如果 ，在最佳蝙蝠中选一个最优个体，再在选择的最优个体附近通过公式（5）生成一个局部解，否则按照公式（4）更新蝙蝠位置。

步骤4: 再生成一个随机数 ， 是[0，1]上的随机数。如果 ，并且此时目标函数的适应度优于步骤 3 中的新解，则接受该位置，并根据公式（6）、（7）调整 （减小）和 （增大）。

步骤5: 对该种群中所有个体的适应度值进行排序，并找到当前最佳 。

步骤6: 重复步骤（2）-（5）。判断是否满足最大迭代次数，然后输出全局最优值。

原理

鲸鱼被认为是世界上最大的哺乳动物。一头成年鲸可以长达 30 米，重 180 吨。这种巨型哺乳动物有 7 种不同的主要物种，如虎鲸，小须鲸，鳁鲸，座头鲸，露脊鲸，长须鲸和蓝鲸等。鲸通常被认为是食肉动物，它们从不睡觉，因为它们必须到海洋表面进行呼吸，但事实上，鲸鱼有一半的大脑都处于睡眠状态。

关于座头鲸最有趣的事情是它们特殊的捕猎方法了。这种觅食行为被称为气泡网觅食法（bubble-net feeding method）。座头鲸喜欢在接近海面的地方捕食磷虾或小鱼。据观察，这种觅食是通过在圆形或类似数字“9”形路径上制造独特的气泡来完成的，如图 1 所示。在 2011 年之前，这一行为仅仅是基于海面观测的。然而，有研究者利用标签传感器研究了这种行为。他们捕获了9头座头鲸身上300个由标签得到的气泡网进食事件。他们发现了两种与气泡有关的策略，并将它们命名为上升螺旋（upward-spirals）和双螺旋（doubleloops）。在前一种策略中，座头鲸会潜到水下 12 米左右，然后开始在猎物周围制造一个螺旋形的泡泡，并游向水面；后一种策略包括三个不同的阶段:珊瑚循环,用尾叶拍打水面以及捕获循环。这里不展开详细描述。

但是气泡网捕食是只有座头鲸独有的一种特殊行为，而鲸鱼优化算法就是模拟了螺旋气泡网进食策略达到优化的目的。

数学建模和优化算法

包围捕食（Encircling prey）

座头鲸可以识别猎物的位置并将其包围。由于最优设计在搜索空间中的位置不是先验已知的，WOA 算法假设当前的最佳候选解是目标猎物或接近最优解。在定义了最佳搜索代理之后，其他搜索代理将因此尝试向最佳搜索代理更新它们的位置。这种行为由下列方程表示：

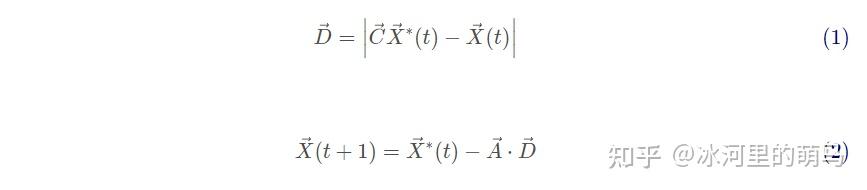
其中t为当前迭代，A和C为系数向量，X?是当前最优解的位置向量，X是当前解的位置向量，||表示绝对值操作，.表示元素相乘。每次迭代过程中有更优解出现时就需要更新X?，A和C计算如下：

其中 在迭代过程中从2线性地下降至0（探索和利用阶段均如此）。r为[0,1]之间的随机向量。

气泡网攻击方式（Bubble-net attacking method）（利用阶段）

共设计了两种方法来对座头鲸的气泡网行为进行建模：

收缩包围机制：通过降低式（3）中的值实现。注意A的波动范围也通过 降低，换句话说，A是一个区间[-a,a]内的随机值，a 随着迭代进行从 2 降为 0。设置A中的随机值在[-1,1]之间，搜索代理的新位置可以定义为代理原始位置与当前最优代理位置之间的任意位置。

螺旋更新位置。如图 3b，该方法首先计算鲸鱼位置 与猎物位置 之间的距离，然后在鲸鱼与猎物位置之间创建一个螺旋等式，来模仿座头鲸的螺旋状移动：

其中 ，表示第i头鲸鱼与猎物（当前最优解）之间的距离，b为常数，定义了对数螺线的形状，l是[-1,1]之间的随机数，符号“.”表示元素相乘。

座头鲸在一个不断缩小的圆圈内绕着猎物游动，同时沿着螺旋形路径游动。为了对这种同时发生的行为进行建模，假设有 50%的可能性在收缩包围机制和螺旋模型之间进行选择，以便在优化过程中更新鲸鱼的位置，数学模型如下：

搜索猎物（Search for prey）(exploration phase)

除了泡泡网方法，座头鲸还会随机寻找猎物，同样基于可变A向量，事实上，座头鲸会根据彼此的位置进行随机搜索，因此使用随机值大于1或小于-1的A来迫使搜索代理远离参考鲸鱼。与利用阶段相反，这里将根据随机选择的搜索代理来更新搜索代理在探索阶段的位置，而不是根据目前为止最优的搜索代理。该机制和 强调了探索，并允许WOA算法执行全局搜索。数学模型如下：

其中 为从当前种群中选择的随机位置向量（表示一头随机鲸鱼）。

原理

海鸥是遍布全球的海鸟，海鸥种类繁多且大小和身长各不相同。 海鸥是杂食动物，吃昆虫、鱼、爬行动物、两栖动物和蚯蚓等。 大多数海鸥的身体覆盖着白色的羽毛，经常用面包屑来吸引鱼群， 用脚发出雨水落下的声音来吸引藏在地下的蚯蚓。海鸥可以喝淡水和盐水，通过眼睛上方的一对特殊腺体，将盐从它们的体内排出。 海鸥以群居式生活，利用智慧来寻找和攻击猎物。 海鸥最重要特征是迁徙和攻击行为，迁徙是动物从一个地方到另一个地方根据季节更替而移动，寻找最丰富的食物来源以便获取足够能量。在迁移期间，动物成群结队地出行。迁徙时每只海鸥的所在位置不同，以避免相互碰撞。 在一个群体中，海鸥可以朝着最佳位置的方向前进，改变自身所在的位置。海鸥经常会攻击候鸟，在进攻时海鸥群体做出螺旋形的运动形态（如图1）。

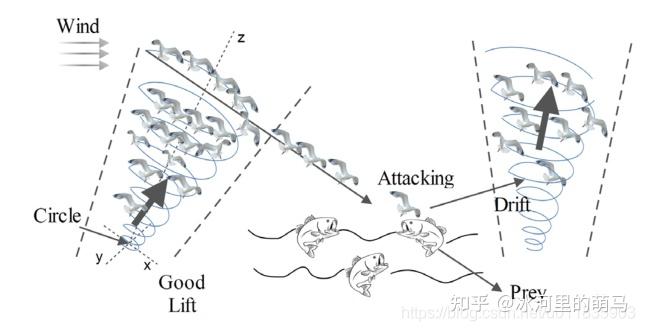
迁徙 ( 全局搜索 )

在迁移过程中， 算法模拟海鸥群如何从一个位置移动到另一个位置。 在这个阶段，海鸥应该满足三个条件：避免碰撞：为了避免与邻居 ( 其他海鸥 ) 碰撞，算法采用附加变量 A 计算海鸥的新位置。

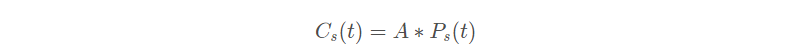
表示不与其他海鸥存在位置冲突的新位置， 海鸥当前位置，t表示当前迭代， A 表示海鸥在给定搜索空间中的运动行为。

可以控制变量 A 的频率，它的值从 2 线性降低到 0 。最佳位置方向：在避免了与其他海鸥的位置重合之后，海鸥会向最佳位置所在的方向移动。

表示最佳位置所在的方向， B 是负责平衡全局和局部搜索的随机数。

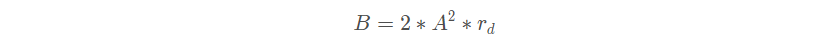
是[0 ， 1]范围内的随机数。靠近最佳位置 : 海鸥移动到不与其他海鸥相撞的位置后，就

向着最佳位置的所在方向进行移动，到达新的位置。

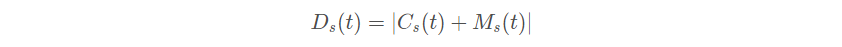
是海鸥的新位置。

攻击 ( 局部搜索 ）

海鸥在迁徙过程中可以不断改变攻击角度和速度， 它们用翅膀和重量保持高度。当攻击猎物时，它们就在空中进行螺旋形状运动。 x 、 y 和 z 平面中的运动行为描述如下：

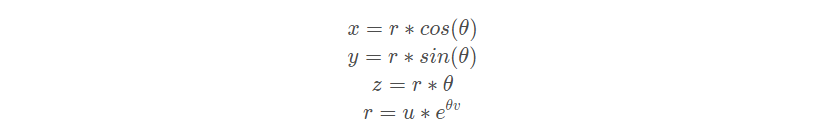
其中 r 是每个螺旋的半径， θ 是[0 ， 2π]范围内的随机角度值。u 和 v 是螺旋形状的相关常数， e 是自然对数的底数。海鸥的攻击位置前面的式子可得：

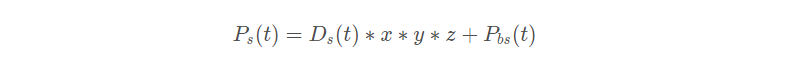
是海鸥的攻击位置。

原理

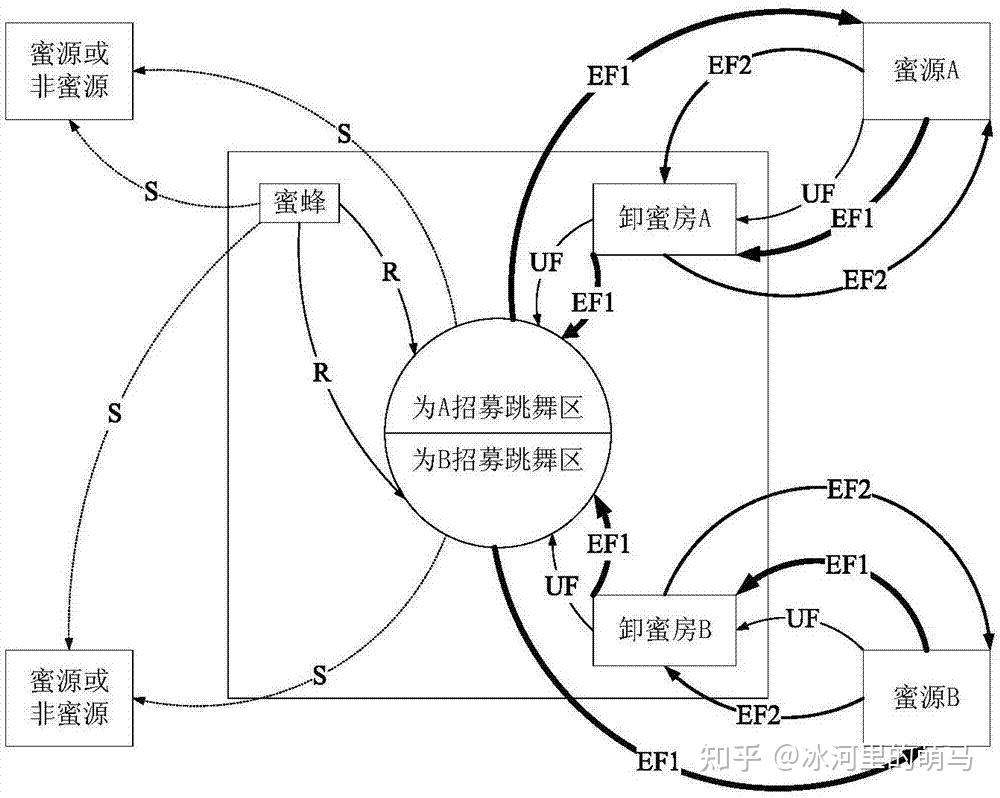
在 ABC 算法里，用蜜源的位置来表示解，用蜜源的花粉数量表示解的适应值。所有的蜜蜂划分为雇佣蜂、跟随蜂、探索蜂三组。雇佣蜂和跟随蜂各占蜂群总数的一半。雇佣蜂负责最初的寻找蜜源并采蜜分享信息，跟随蜂负责呆在蜂巢里根据雇佣蜂提供的信息去采蜜，探索蜂在原有蜜源被抛弃后负责随机寻找新的蜜源来替换原有的蜜源。与其他群智能算法一样，ABC 算法是迭代的。对蜂群和蜜源的初始化后，反复执行三个过程，即雇佣蜂、跟随蜂、探索蜂阶段，来寻找问题的最优解。每个阶段描述如下:

蜂群的初始化

对 ABC 算法的参数进行初始化，这些参数有蜜源数 、蜜源确定被抛弃的次数 、迭代终止次数。在标准 ABC 算法里，蜜源的数目 与雇佣蜂数相等，也与跟随蜂数相等。产生某个蜜源的公式为:

其中: 代表第 个蜜源 的第 维度值， 取值于 取值于 ， 和 分别代表第j 维的最小值和最大值。初始化蜜源就是对每个蜜源的所有维度通过以上公式赋一个在取值范围内的随机值，从而随机生成 个最初蜜源。

雇佣蜂阶段

在雇佣蜂阶段，雇佣蜂用以下公式来寻找新蜜源:

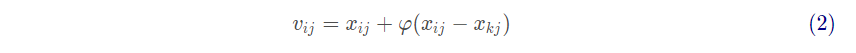
其中: 代表邻域蜜源，取值于 且k不等于i ； 是取值在[-1,1]的随机数，通过式(2)得到新蜜源后，利用贪婪算法，比较新旧蜜源适应值，选择优者。

跟随蜂阶段

雇佣蜂阶段结束，跟随蜂阶段开始。在该阶段，雇佣蜂在舞蹈区分享蜜源信息。跟随蜂分析这些信息，采用轮盘赌策略来选择蜜源跟踪开采，以保证适应值更高的蜜源开采的概率更大。跟随蜂开采过程与雇佣蜂一样，利用式(2)找寻新蜜源，并留下更优适应者。蜜源拥有参数 ，当蜜源更新被保留时， 为0反之， l加 1。从而 能统计出一个蜜源没有被更新的次数。

探索蜂阶段

如果一个蜜源经过多次开采没被更新，也就是 值过高，超过了预定阈值 ，那么需抛弃这个蜜源，启动探索蜂阶段。这体现了 ABC 里自组织的负反馈和波动属性 。在该阶段里，探索蜂利用式(3)随机寻找新的蜜源来代替被抛弃蜜源。

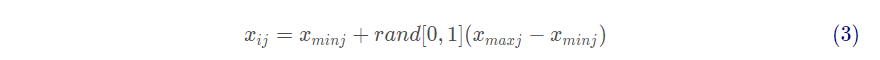
算法流程

人工蜂群算法流程

1.初始化算法参数，生成蜜蜂初始位置

2.雇佣蜂计算适应度值，比较并保存最优值

3.跟随蜂选择雇佣蜂更新蜜源位置，计算适应度值，保存最佳值

4.若有侦察蜂出现，则重新生成初始位置并执行更新选优，否则继续执行5

5.若迭代次数小于预设的迭代次数，则转到2；否则输出最优解

原理

狼群中有α、β、γ三只狼做头狼，其中α是狼王，β、γ分别排第二、第三，β、γ都要听α的，γ要听β的。这三匹狼指导者其他的狼寻找猎物。狼群寻找猎物的过程就是我们寻找最优解的过程。GWO具体优化过程包含了社会等级分层、跟踪、包围和攻击猎物和寻找猎物。但其核心行为只有捕猎。为了模拟灰狼的搜索行为，假设α、β、γ具有较强识别潜在猎物的能力，因此，在每次迭代过程中，保留当前种群中最好的三只狼（α、β、γ），然后根据他们的位置信息来更新其他搜索代理的位置。

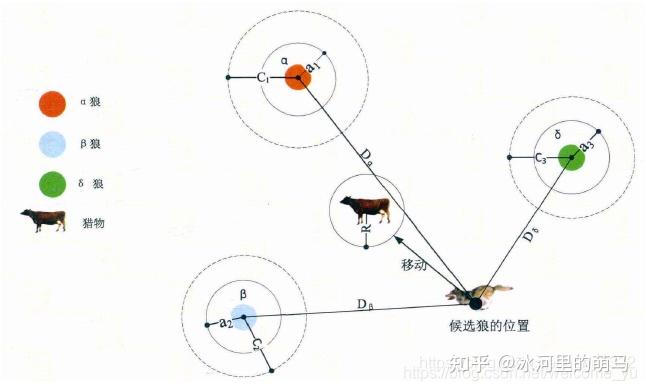
灰狼的社会等级在群体狩猎过程中发挥着重要的作用，捕食的过程在 α 的带领下完成。灰狼的狩猎包括以下 3个主要部分：

1）跟踪、追逐和接近猎物；

2）追捕、包围和骚扰猎物，直到它停止移动；

3）攻击猎物

包围猎物

在狩猎过程中，将灰狼围捕猎物的行为定义如下：

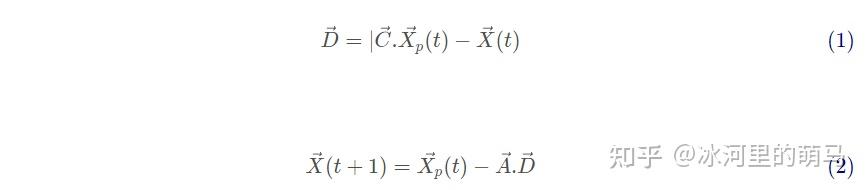
式（1）表示个体与猎物间的距离，式（2）是灰狼的位置更新公式。其中,t 是目前的迭代代数，A和C是系数向量， 和 分别是猎物的位置向量和灰狼的位置向量。A和C的计算公式如下：

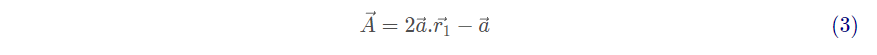
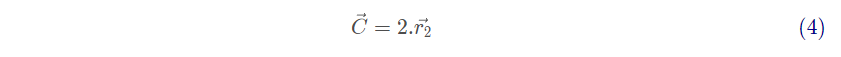
其中， 是收敛因子，随着迭代次数从2线性减小到0， 和 的模取[0,1]之间的随机数。

狩猎

灰狼能够识别猎物的位置并包围它们。当灰狼识别出猎物的位置后，β 和 δ 在 α 的带领下指导狼群包围猎物。在优化问题的决策空间中，我们对最佳解决方案（猎物的位置）并不了解。因此，为了模拟灰狼的狩猎行为，我们假设 α ，β 和 δ 更了解猎物的潜在位置。我们保存迄今为止取得的３个最优解决方案，并利用这三者的位置来判断猎物所在的位置，同时强迫其他灰狼个体（包括 ω ）依据最优灰狼个体的位置来更新其位置，逐渐逼近猎物。狼群内个体跟踪猎物位置的机制如图２所示。

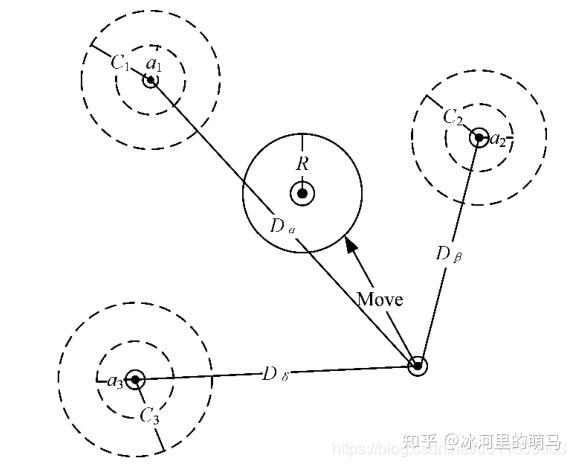
灰狼个体跟踪猎物位置的数学模型描述如下:

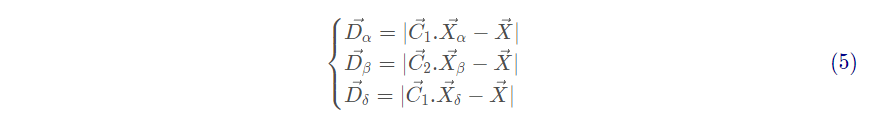
其中， 分别表示分别表示 α ， β 和 δ 与其他个体间的距离。 分别代表 α ， β 和 δ 的当前位置； 是随机向量， 是当前灰狼的位置。

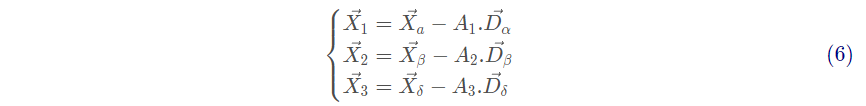
式(6)分别定义了狼群中 ω 个体朝向 α ，β 和 δ 前进的步长和方向，式(7)定义了 ω 的最终位置。

攻击猎物（开发）

当猎物停止移动时，灰狼通过攻击来完成狩猎过程。为了模拟逼近猎物，a的值被逐渐减小，因此A的波动范围也随之减小。换句话说，在迭代过程中，当a的值从2线性下降到0时，其对应的A的值也在区间[-a,a]内变化。如图3a所示，当A的值位于区间内时，灰狼的下一位置可以位于其当前位置和猎物位置之间的任意位置。当 时，狼群向猎物发起攻击（陷入局部最优）。

搜索猎物（勘探）

灰狼根据 α ,β 和 δ 的位置来搜索猎物。灰狼在寻找猎物时彼此分开，然后聚集在一起攻击猎物。基于数学建模的散度，可以用A大于1 或小于-1 的随机值来迫使灰狼与猎物分离，这强调了勘探（探索）并允许 GWO 算法全局搜索最优解。如图3所示， 强迫灰狼与猎物（局部最优）分离，希望找到更合适的猎物（全局最优）。GWO 算法还有另一个组件 来帮助发现新的解决方案。由式(4)可知， 是[0,2]之间的随机值。Ｃ表示狼所在的位置对猎物影响的随机权重， 表示影响权重大，反之，表示影响权重小。这有助于 GWO算法更随机地表现并支持探索，同时可在优化过程中避免陷入局部最优。另外，与A不同C的是非线性减小的。这样，从最初的迭代到最终的迭代中，它都提供了决策空间中的全局搜索。在算法陷入了局部最优并且不易跳出时，C的随机性在避免局部最优方面发挥了非常重要的作用，尤其是在最后需要获得全局最优解的迭代中。

原理

樽海鞘优化算法(Salp Swarm Algorithm,SSA)是由澳大利亚的Seyedali Mirjalili于2017年提出的一种新型优化算法，该算法模拟了樽海鞘在海洋中航行和觅食时的群集行为，樽海鞘属樽海鞘科，体透明，呈桶状，其组织与水母非常相似，如图1所示。尊海鞘最有趣的行为之一是它们的群体行为，在深海中，樽海鞘经常形成一个称为樽海鞘链的群体，如图：

樽海鞘移动的策略

为了对樽海鞘进行数学建模，首先将种群分为两个组：领导者和追随者。领导者是链中最前面的樽海鞘，而剩余其他的就都是追随者。同其他基于种群的优化技术一样，在n维搜索空间中定义樽海鞘的位置，其中n维给定问题的变量个数。因此所有樽海鞘的位置都存储于二维矩阵x中。同时假设在搜索空间存在食物源F ，作为种群的目标。通过以下公式来更新领导者的位置：

其中 表示第一个尊海鞘（领导者）在第 j 维位置， 是食物源在第 j 维上的位置， 和 分别是第 j 维上的上界和下界， 和 为随机数。

式(1)表明领导者仅更新与食物源的相对位置，系数 式SSA中最重要的参数，因为其用于平衡探索和利用：

其中 l 为当前迭代次数，L为最大迭代次数。利用如下公式对追随者的位置进行更新：

其中 , 表示第i个追随者樽海鞘在第j维上的位置，t 为时间，v0是初始速度，其中 。

由于在优化中时间就是迭代次数，所以迭代时间之差就是1，考虑到 ，上式可以表达为：

式中： 和 分别是第 d 维中更新后的追随者的位置和更新前追随者的位置。

算法流程：

1初始化种群。根据搜索空间每一维的上界与下界，利用式(1)初始化一个规模为N ×D 的樽海鞘群。

2计算初始适应度。计算 N 个樽海鞘的适应度值。

3选定食物。由于实际定位时我们不知道目标(即食物)的位置，因此，将樽海鞘群按照适应度值进行排序，排在首位的适应度最优的樽海鞘的位置设为当前食物位置。

4选定领导者与追随者。选定食物位置后，群体中剩余N ?1 个樽海鞘，按照樽海鞘群体的排序，将排在前一半的樽海鞘视为领导者，其余樽海鞘视为追随者。

5位置更新。首先根据式(2)更新领导者的位置，再根据式(6)更新追随者的位置。

6计算适应度。计算更新后的群体的适应度。将更新后的每个樽海鞘个体的适应度值与当前食物的适应度值进行比较，若更新后樽海鞘的适应度值优于食物，则以适应度值更优的樽海鞘位置作为新的食物的位置。

7重复步骤4)-步骤6)，直到达到一定迭代次数或适应度值达到终止门限，满足终止条件后，输出当前的食物位置作为目标的估计位置。

原理

蚁狮属于蚁蛉科，为脉翅目类昆虫。蚁狮的生命周期包括两个主要阶段:幼虫和成虫，自然总寿命可达3年，主要发生在幼虫(成年期为3-5周)。它们的名字源于它们独特的捕猎行为和它们最喜爱的猎物。ALO 算法核心思想是模拟蚁狮捕猎蚂蚁的狩猎机制以实现全局寻优。蚁狮在捕猎前会在在沙质土中利用其巨大的下颚挖出一个漏斗状的陷阱，并藏在陷阱底部等待猎物到来。一旦随机游走的蚂蚁落入陷阱时，蚁狮迅速将其捕食，随后重新修缮陷阱等待下一次捕猎。ALO 算法通过数值模拟实现蚂蚁和蚁狮之间的相互作用将问题优化:引入蚂蚁的随机游走实现全局搜索，通过轮盘赌策略和精英策略保证种群的多样性和算法的寻优性能。蚁狮相当于优化问题的解，通过猎捕高适应度的蚂蚁实现对近似最优解的更新和保存。

蚂蚁游走策略

ALO算法模拟了蚁狮和陷阱中的蚂蚁之间的交互，为了模拟这种交互作用，蚂蚁需要在搜索空间中移动，而蚁狮则可以捕猎它们。由于蚂蚁在自然界中寻找食物时是随机移动的，因此通过选择一个随机行走来模拟蚂蚁的运动：

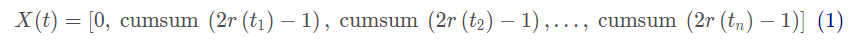
其中cumsum计算了累积和，n为最大迭代次数，t表示随机游走的步数（即迭代），r(t)通过以下定义的随机函数：

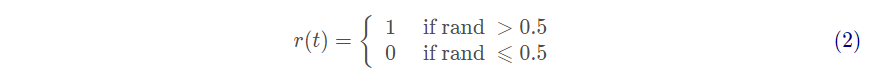
其中rand为[0,1]内服从均匀分布的随机数。由于可行域存在边界，不能直接用式(1)更新蚂蚁的位置。为确保蚂蚁在可行域范围内随机游走，需根据式(3)对其进行归一化

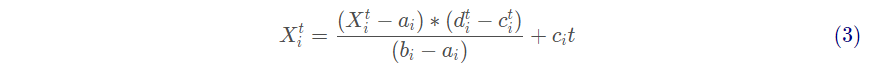
式中: 为第 i 维变量随机游走的最小值; 为第i维变量随机游走的最大值； 为第 i 维变量再第 t 次迭代的最小值； 为第 i 维变量在第 t 次迭代最大值。

蚁狮对蚂蚁随机游走的影响

蚁狮制造的陷阱会影响蚂蚁随机游走的路线，为对此假设进行数学建模，提出

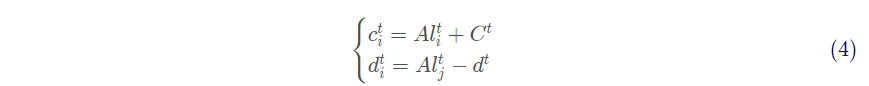
式中:ct为所有变量在第t 次迭代的最小值; dt为所有变量在第t 次迭代的最大值 为被选定的第 j 只蚁狮在第t 次迭代的位置。

自适应机制

通过轮盘赌策略选择某只蚂蚁具体被哪只蚁狮捕食，每只蚂蚁只能被一只蚁狮捕食，而适应度越高的蚁狮捕获蚂蚁的概率越大。另外，蚂蚁一旦落入蚁狮制造的陷阱，蚁狮就会向陷阱边缘抛沙以防止蚂蚁逃脱。此时，蚂蚁随机游走的范围将急剧缩小。通过下列方程模拟这种现象。

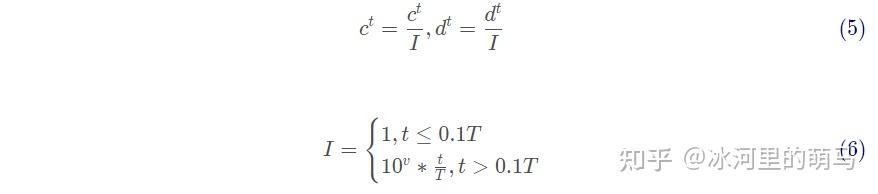
式中:I 为比例系数；T为最大迭代次数；v为一个随着迭代次数增大而变化的数。当蚂蚁的适应度值比蚁狮小时，则认为蚁狮将其捕获，此时蚁狮会根据蚂蚁的位置来更新位置

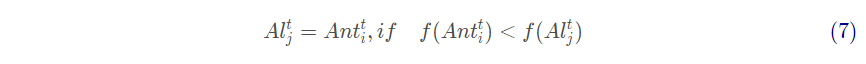
式中: 为第i 只蚂蚁在第t 次迭代的位置;f 为适应度函数。

精英策略

每次迭代后，选择适应度最好的蚁狮作为精英蚁狮。第t 只蚂蚁在第 次迭代的位置由式(8)确定

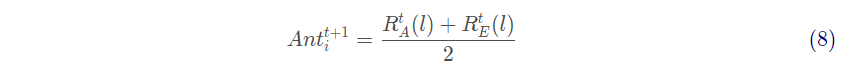
式中： 为蚂蚁在一只由轮盘赌在第t 次迭代选择到的蚁狮周围随机游走第l 步产生的值； 为蚂蚁在第t代的精英蚁狮周围随机游走第l 步产生的值。l 为蚂蚁随机游走步数内的任何值。

算法步骤

1数据初始化。确定蚂蚁和蚁狮的数量以及变量维数，在可行域内随机初始化它们的位置，并计算相应的适应度值。

2确定精英蚁狮。选择初始化后蚁狮种群中适应度最好的作为精英蚁狮。

3通过轮盘赌为每只蚂蚁选择一只蚁狮，根据蚁狮位置更新 的值，并使该蚂蚁按照式(1)、式(3)在蚁狮及精英蚁狮附近随机游走，最后按式(8)取平均值作为蚂蚁的位置。

4每次迭代后重新计算蚂蚁和蚁狮适应度值，根据蚂蚁的位置和适应度更新蚁狮位置，适应度最好的位置为新精英蚁狮的位置。

5判断是否到达最大迭代次数，若到达则输出结果并结束迭代，否则重复步骤 (3)

原理

在FA 中 , 萤火虫发出光亮的主要目的是作为一个信号系统 , 以吸引其他的萤火虫个体 , 其假设为 : 1) 萤火虫不分性别 , 它将会被吸引到所有其他比它更亮的萤火虫那去 ; 2) 萤火虫的吸引力和亮度成正比 , 对于任何两只萤火虫 , 其中一只会向着比它更亮的另一只移动 , 然而 , 亮度是随着距离的增加而减少的 ;3) 如果没有找到一个比给定的萤火虫更亮 , 它会随机移动 。

如上所述 , 萤火虫算法包含两个要素 , 即亮度和吸引度 . 亮度体现了萤火虫所处位置的优劣并决定其移动方向 , 吸引度决定了萤火虫移动的距离 , 通过亮度和吸引度的不断更新 , 从而实现目标优化 . 从数学角度对萤火虫算法的主要参数进行如下描述 ：

萤火虫的相对荧光亮度

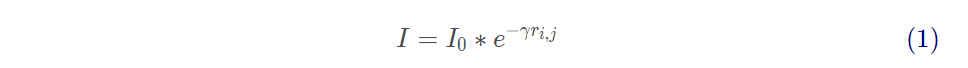
其中 , 为萤火虫的最大萤光亮度 , 与目标函数值相关 , 目标函数值越优自身亮度越高 ;γ为光强吸收系数 , 荧光会随着距离的增加和传播媒介的吸收逐渐减弱 ; 为萤火虫 与 之间的空间距离 。

萤火虫的吸引度

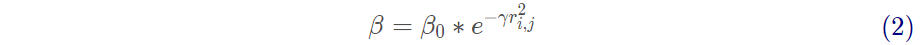
其中 , 为最大吸引度 ; 为光强吸收系数 ;

萤火虫 i 被吸引向萤火虫 j 移动的位置更新公式如式 (3) 所示 :

其中 , 为萤火虫 和 所处的空间位置 ; 为步长因子 ; 为[0,1]上服从均匀分布的随机数 。

算法步骤如下：

1初始化萤火虫算法参数.

2计算各萤火虫的亮度并排序得到亮度最大的萤火虫位置.

3判断迭代是否结束：判断是否达到最大迭代次数 T ，达到则转（4），否则转（5）.

4输出亮度最大的萤火虫位置及其亮度.

5 更新萤火虫位置：根据式（3）更新萤火虫的位置，对处在最佳位置的萤火虫进行随机扰动，搜索次数增加1 ，转（2），进行下一次搜索.

原理

新型的仿生学算法—鸡群优化算法，它模拟群的等级制度和鸡群的群体活动行为。 在特殊的等级制度下鸡群中不同鸡种搜寻食物时存在着竞争。公鸡搜索食物能力强，适应值小；母鸡其次；小鸡搜索食物能力最弱，适应值最大。鸡群按公鸡个数来分组，每组由一只公鸡、一些母鸡和小鸡组成，有几只公鸡就有几组。分组中，公鸡搜索能力最强，处于统治地位，适应值最小；搜索能力稍差的母鸡紧跟在公鸡周围搜索食物，适应度值稍大；其中一些母鸡还带领小鸡，小鸡搜索能力最差，只在母鸡周围搜索食物，适应度值最大，实现局部搜索功能。在等级制度下，分组中公鸡的统治关系和母鸡 - 小鸡的母子关系将会改变。通过适应度值来建立这种等级秩序，并随机分组建立公鸡与母鸡的关系，随机建立母鸡—小鸡的母子关系。鸡群中，适应度值越小的个体越占有优势，可以优先获得食物，并且统领适应度值大的个体。 适应度值最小的个体对应鸡群中的公鸡，稍大的对应于母鸡，最大的对应于小鸡，在这种等级秩序下它们以组为单位合作，并按照各自的运动规律更新位置，进行搜索，最终搜索到最佳的觅食位置，即得到最优解。

位置更新策略

因为不同的鸡种有不同的运动规律， 因此，以下 3 种个体的位置更新策略各不相同。

公鸡的位置更新策略

适应度好的公鸡能够在更大的范围内搜索食物，而且比适应度差的公鸡能够优先获得食物实现全局搜索，它的位置更新受随机选取的其他公鸡位置的影响，则更新策略见式（1）-（2）

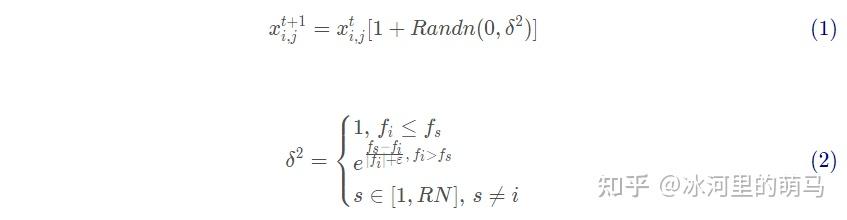
式 (1)-(2) 中：第i 只公鸡位置的第 j 维的值表示为，s 表示当前的迭代次数，表示服从期望值为0 ，方差值为 2 的正态分布随机数，第i 只公鸡的适应度为 ?，随机选取公鸡s 的适应度为 ， 分母中加上无穷小数ε，避免除数为零。

母鸡的位置更新策略

母鸡跟随伙伴公鸡搜索食物，位置更新受伙伴公鸡位置影响。由于母鸡的偷食行为，位置更新又与其它公鸡和母鸡有关系，则更新策略见式 (3)-(5) 。

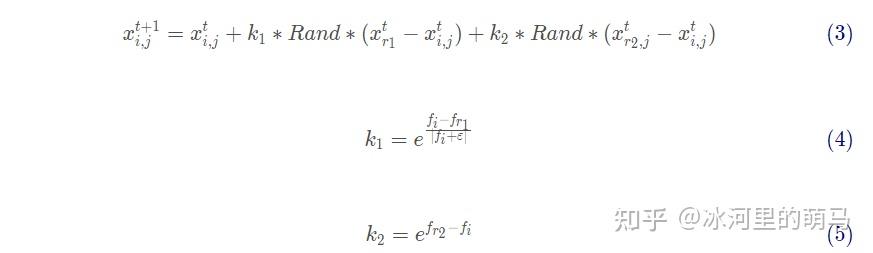
式 (3)-(5) 中： Rand 是一个服从[0,1]均匀分布的随机数，该母鸡的伙伴公鸡 的适应度为 ， 表示其伙伴公鸡对其的影响因子，其他公鸡和母鸡中随机选取个体 的适应度值为 ， 为其他鸡对其的影响因子。

小鸡的位置更新策略

小鸡在其母亲周围搜寻食物，它的搜索能力最差，位置受到母亲公鸡的影响，则更新策略见式 (6) 。

中：母亲母鸡m位置的第j维数值为 ，j ，母亲母鸡的位置对小鸡位置的影响因子为P ，其为随机函数随机生成，取值范围一般为 (0,2) 。

算法流程

步骤如下：

1. 初始化参数。 初始配置算法参数，主要是鸡群的大小、迭代的次数、种群关系的更新频率、个体位置的维度、公鸡母鸡小鸡在鸡群中的比例等。
2. 初始化鸡群。 鸡群按适应度值排序分级，公鸡为前 个个体小鸡为最末 个个体，其余均为母鸡。将鸡群按公鸡数分成 个组，母鸡随机分配到个组中，确定公鸡和母鸡的伙伴关系。 随机选取 个母鸡，随机统领小鸡，确定母鸡小鸡的母子关系。
3. 迭代开始，先判断是否需要更新分组，是否需要更新鸡群中的关系，需要则更新鸡群分组和鸡群中的关系；否则，公鸡、母鸡和小鸡的位置分别按照各自的位置更新策略， 对各自位置逐个进行更新，同时计算更新位置的适应度值。
4. 个体位置更新。 新位置的适应度值与原位置适应度值相比，如果新的位置的适应度值小就更新个体位置，否则就保持原来的位置不变。
5. 达到最大迭代次数后停止迭代，并输出最优解，否则回到第 3 步，循环迭代进行搜索。

以上是为大家分享的内容，部分内容参考来自csdn，大家想了解更多的也可以去csdn查阅相关算法原理及步骤。